So yesterday I headed over to City University London
 for the first time ever, it's near Angel station in London and it actually has buildings that can compete with King's Strand campus for ugliness (see right for the cheery city logo attempting to liven up the Tait building where the mathematics department is). However, once inside, all was forgiven, not only for the simple reason that we can no longer see the architecture but also because I was looking forward to attending a rare group theory seminar in London. Infrequently do the theory group talks become group theory talks, but yesterday was just such a special day!
for the first time ever, it's near Angel station in London and it actually has buildings that can compete with King's Strand campus for ugliness (see right for the cheery city logo attempting to liven up the Tait building where the mathematics department is). However, once inside, all was forgiven, not only for the simple reason that we can no longer see the architecture but also because I was looking forward to attending a rare group theory seminar in London. Infrequently do the theory group talks become group theory talks, but yesterday was just such a special day!Robert Wilson from Queen Mary, University of London was talking under the title "Finite Groups with Small Automorphism Groups". Robert's homepage contains some links to the text of some of his previous talks, as well as a link to some lecture notes on finite groups which are on their way to becoming a nice looking book. The topic of today's talk was based on Robert's paper with John Bray, the pdf of which can be found here.
Robert's talk was wonderfully pedagogical, beginning with the title he made sure everyone in the room new what a group is and what an automorphism is. He said it was an article of faith for him that all groups are finite :) The only real question was what small meant. So an automorphism of a group, G, is an isomorphism, A, of G: G->G. Robert took the time to show us that set of all automorphisms of a group is also a group, denoted Aut(G), i.e. take A, B, C to be elements of Aut(G), then clearly AB is in Aut(G) and A(BC)=(AB)C, while since the Id and the inverse maps are all isomorphisms too, Aut(G) is a group. We were then introduced to a subgroup of Aut(G), called the group of inner automorphisms, or Inn(G), so-called because these automorphism actions are constructed from elements "in" G. Take g in G, then define an automorphism:
 This is clearly a map from G to G and it's an isomorphism since:
This is clearly a map from G to G and it's an isomorphism since: It turns out that inner sutomorphisms form a normal subgroup of G, as, for B in Aut(G),
It turns out that inner sutomorphisms form a normal subgroup of G, as, for B in Aut(G),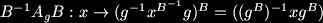 i.e.
i.e.  So Inn(G) is a normal subgroup of Aut(G).
So Inn(G) is a normal subgroup of Aut(G).Robert also showed us the outer automorphism group, Out(G), which is defined as a quotient group,
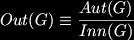 Next we had a proposition, that if the inner automorphism was the identity automorphism, then the group element, g, that it was constructed out of would be in the centre of the group, Z(G),
Next we had a proposition, that if the inner automorphism was the identity automorphism, then the group element, g, that it was constructed out of would be in the centre of the group, Z(G),  So that,
So that,  Then we came to the crucial examples. First let the group be a cyclic group of order n, i.e. integers under addition modulo n, which is generated by the element a. That is,
Then we came to the crucial examples. First let the group be a cyclic group of order n, i.e. integers under addition modulo n, which is generated by the element a. That is,  Now suppose B is an automorphism of this group, so that,
Now suppose B is an automorphism of this group, so that, Now since B is an automorphism then the whole of the cyclic group must be reproduced by its action. This places the restriction on the possible values k can take; k must be coprime with n (their greatest common divisor must be one). So the number of automorphisms of G, the order of Aut(G), is simply the number of integers less than n which are coprime with n. The function that counts this number is yet another of Euler's and is called the Euler totient function denoted
Now since B is an automorphism then the whole of the cyclic group must be reproduced by its action. This places the restriction on the possible values k can take; k must be coprime with n (their greatest common divisor must be one). So the number of automorphisms of G, the order of Aut(G), is simply the number of integers less than n which are coprime with n. The function that counts this number is yet another of Euler's and is called the Euler totient function denoted 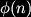 . For the cyclic group the order of the automorphism group, given by the Euler totient function, is less than the order of the group.
. For the cyclic group the order of the automorphism group, given by the Euler totient function, is less than the order of the group.Now consider a second example, taking G to be a non-abelian simple group, i.e. it has no normal subgroups besides the trivial ones of the identity and the group G itself. In this case the centre of G is just the identity element, so that,
 So that, in this case,
So that, in this case, So now we find out what was meant by "small" in the title; if the order of Aut(G) is greater than the order of G we say that the automorphism group is large, and if it is smaller than the order of G then we say that it is small.
So now we find out what was meant by "small" in the title; if the order of Aut(G) is greater than the order of G we say that the automorphism group is large, and if it is smaller than the order of G then we say that it is small.Robert showed us some properties of the totient function, which are really useful and can all be found in the wikipedia article, before describing his work with Bray. He told us about Kourovka notebooks, which contain open problems in group theory, where it was in volume 15, question 43 by Deaconescu whether,
 might be true for all finite groups and whether equality might be attained only for cyclic groups. Together with Bray he found a simple group for which these properties didn't hold. For what it's worth, the group is the twelve-fold cover of
might be true for all finite groups and whether equality might be attained only for cyclic groups. Together with Bray he found a simple group for which these properties didn't hold. For what it's worth, the group is the twelve-fold cover of  , which is a simple group of order 22.21.20.16.3=443520. How did they do this? Well Robert said he picked up his copy of the Atlas of Finite Groups (online atlas) and when he got to page three he found the counterexample he needed using the formulae he told us in the talk, as well as the properties of the Euler totient function, and hey presto! They also began to wonder just how small can these small (by which I mean the ratio of the orders of Aut(G) to G) automorphism groups be, and they discovered that they can be arbitrarily small.
, which is a simple group of order 22.21.20.16.3=443520. How did they do this? Well Robert said he picked up his copy of the Atlas of Finite Groups (online atlas) and when he got to page three he found the counterexample he needed using the formulae he told us in the talk, as well as the properties of the Euler totient function, and hey presto! They also began to wonder just how small can these small (by which I mean the ratio of the orders of Aut(G) to G) automorphism groups be, and they discovered that they can be arbitrarily small. So there you go. A very nice pedagogical talk, which perhaps felt like the beginning of two talks, and a lesson in the art of proactive mathematics.






