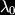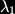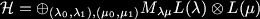Perhaps due to the time constraint, quantities were not defined and many ideas were assumed to be known by the audience. Unfortunately there is much work for me to do. At one point she paused and said to the audience:
Perhaps due to the time constraint, quantities were not defined and many ideas were assumed to be known by the audience. Unfortunately there is much work for me to do. At one point she paused and said to the audience: "So far I was a bit sketchy...but this is something you can read. This is a known result."Well this is true enough, so here are the references for Kallosh's first talk (just 1 hour):
It would have been good to know these papers well before the talk began and as you can imagine the school degenerated to a workshop for the experts during this talk. However there were plenty of interesting things for us beginners to pick up. Such as that N=2 special geometry is useful and that symplectic invariants are useful. I'll try and reproduce my beginner's conception of special geometry in this post, mostly with the help of Christiann Hofman's masters' thesis, Dualities in N=2 String Theory (you can find the link near the bottom of the page).Black holes and critical points in moduli space by S. Ferrara, G. W. Gibbons and R. Kallosh Non-Supersymmetric Attractors in String Theory by P.K. Tripathy and S. P. Trivedi The non-BPS black hole attractor equation by R. Kallosh, N. Sivanandam and M. Soroush The Symplectic Structure of N=2 Supergravity and its central extension by A. Ceresole, R. D'Auria and S. Ferrera E(7) Symmetric Area of the Black Hole Horizon by Renata Kallosh, Barak Kol STU Black Holes and String Triality by Klaus Behrndt, Renata Kallosh, Joachim Rahmfeld, Marina Shmakova, Wing Kai Wong Calabi-Yau Black Holes by Marina Shmakova
Special geometry is the name given for the geometry associated to the scalar couplings of the vector and hypermultiplets of theories involving 8 supercharges, although the original use of the name was restricted to N=2, vector multiplets and four dimensions. Recall that the vector multiplet is an irreducible multiplet of super Yang-Mills theory, it is the enhancement of the gauge field to the supersymmetric setting, and has field content:
 Where X is a complex scalar, omega is a pair of spinors, Y is a triplet of scalars (arranged in an anitsymmetric 2 by 2 matrix) and A is a real gauge boson. For reference the hypermultiplet, when there are no central charges contains the fields:
Where X is a complex scalar, omega is a pair of spinors, Y is a triplet of scalars (arranged in an anitsymmetric 2 by 2 matrix) and A is a real gauge boson. For reference the hypermultiplet, when there are no central charges contains the fields: Here, A is a pair of scalar doublets, and zeta is a pair of spinors. When we include gravity in our supersymmetric gauge theory setting we find the metric is enhanced to the gravity multiplet, or Weyl multiplet, consisting of the metric and two fermionic fields of spin 3/2 called gravitini. These gravitational fields can couple to the content of the vector and hyper multiplets. Furthermore an additional vector multiplet is required if we wish to break auxillary gauge symmetries (see Lagrangians of N=2 supergravity-matter systems by de Wit, Lauwers and Van Proeyen). Only the vectors have physical significance, the remainder of the multiplets are auxillary fields. So if we commence with n vector multiplets from our super Yang-Mills theory, and then we include gravity to construct a sensible local theory, we find we require n+1 gauge fields. These gauge fields are the equivalents of our familiar Maxwell gauge field in electromagnetism, and including the dual fields we have 2(n+1) fields which are transformed into each other by the action of the symplectic group Sp(2n+2,R). The flux integrals of the field strengths and their duals give us electric, q, and magnetic, p, charges, and the symplectic transformation is interpreted as the generalization of electric-magnetic duality. So far, so good. But we neglected to mention that we also have n scalar fields which do not transform in such a well-mannered way under the symplectic group action. A suitable projective coordinate reparameterisation (giving us n+1 scalars) will, however, do the job, see Mohaupt's review Strings, higher curvature corrections and black holes for the overview. The scalars of the Lagrangian may be thought of as coordinates and, under the restrictions of supersymmetry, the geometry of the complex symplectic vector space C(2n+2)associated to the scalar coordinates is called special geometry. We end up with coordinates on our manifold, coming from the prepotential and the projective coordinate which do transform as a symplectic vector. However symplectic geometry is a little different from Riemannian geometry, for example symplectic manifolds have no local invariants like curvature.
Here, A is a pair of scalar doublets, and zeta is a pair of spinors. When we include gravity in our supersymmetric gauge theory setting we find the metric is enhanced to the gravity multiplet, or Weyl multiplet, consisting of the metric and two fermionic fields of spin 3/2 called gravitini. These gravitational fields can couple to the content of the vector and hyper multiplets. Furthermore an additional vector multiplet is required if we wish to break auxillary gauge symmetries (see Lagrangians of N=2 supergravity-matter systems by de Wit, Lauwers and Van Proeyen). Only the vectors have physical significance, the remainder of the multiplets are auxillary fields. So if we commence with n vector multiplets from our super Yang-Mills theory, and then we include gravity to construct a sensible local theory, we find we require n+1 gauge fields. These gauge fields are the equivalents of our familiar Maxwell gauge field in electromagnetism, and including the dual fields we have 2(n+1) fields which are transformed into each other by the action of the symplectic group Sp(2n+2,R). The flux integrals of the field strengths and their duals give us electric, q, and magnetic, p, charges, and the symplectic transformation is interpreted as the generalization of electric-magnetic duality. So far, so good. But we neglected to mention that we also have n scalar fields which do not transform in such a well-mannered way under the symplectic group action. A suitable projective coordinate reparameterisation (giving us n+1 scalars) will, however, do the job, see Mohaupt's review Strings, higher curvature corrections and black holes for the overview. The scalars of the Lagrangian may be thought of as coordinates and, under the restrictions of supersymmetry, the geometry of the complex symplectic vector space C(2n+2)associated to the scalar coordinates is called special geometry. We end up with coordinates on our manifold, coming from the prepotential and the projective coordinate which do transform as a symplectic vector. However symplectic geometry is a little different from Riemannian geometry, for example symplectic manifolds have no local invariants like curvature.If, like me, you have never come across any of this technology before you can see that there is plenty of work to do. Especially in picking up terminology and generic constructions. But don't despair! Take heart, all the experts at the school in Frascati presented some very pretty results (I was able to understand this from the joy in their eyes - inc omcing to this conclusion I have assumed the sanity of the speakers...) and it would seem the end result is worth the work.