Classifying Rational Conformal Field Theories

Yesterday afternoon was quite a chilly day in London, the kind of day when being crammed into a packed and warm lecture room below ground level in the basement of Queen Mary college from where you can hear the tube rattle by was quite an attractive prospect. So at three in the afternoon yesterday that's where I and other London theoretical physicists gathered to hear Terry Gannon talk about "The classification of RCFTs".

First off, it gives me great pleasure to report to you that the "damn book" is finished :) after five years of hard slog Terry's book, Moonshine Beyond the Monster and available to buy from the 31st August, 2006. Hurrah. There's an excellent documentary by Ken Burns on the American Civil War that took longer to make than the war itself, I have no doubt that it will take me inestimably longer to understand this 538 page book than it took to write. Fortunately noone died in the making of the book, to the best of my knowledge. For some history of the Monster see Terry's Monstrous Moonshine: The First Twenty-Five Years.

Terry described his approach to trying to classify Rational Conformal Field Theories (you could look at Wikipedia for a brief definition of a RCFT, or a much better idea might be to start learning about CFT from scratch with Paul Ginsparg's Les Houches lectures, Applied Conformal Field Theories or Krzysztof Gawedzki's Lectures on Conformal Field Theory) by searching for invariants of the chiral algebra, or Frobenius algebra, that underlies the RCFT. By way of comparison, Terry said that the very succesful classification of the Lie algebras rested upon the invariant of the Dynkin diagram. But what invariants are worth considering, whose discovery will tell us most of the information about the algebra? Terry suggested two:

modular invariants (i.e. partition function on the torus)

NIM representations (i.e. partition function on the cylinder)

But he only had enough time to talk a little about the first and describe to us the modular functions that appear.

To commence one must settle upon a chiral algebra, or a vertex operator algebra, and Terry told us that some very nice choices are the affine Kac-Moody algebras (see Fuchs' Lectures on conformal field theory and Kac-Moody algebras section 16 for the definitions). A level, k, must also be picked. We were told that one way to imagine a chiral algebra is as a complexification, or 2-dimensionalisation, of a Lie algebra. If we denote all the objects appearing in a Lie algebra by a tree diagram, having all the properties of the Lie bracket at the branch (i.e. antisymmetric...) then the complexified version of the algebra turns each of the branches of the tree diagram into a cylinder: 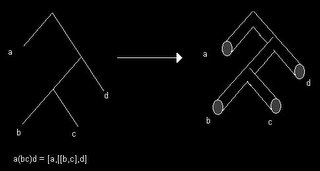For more about this way of complexifying to get loop algebras we were referred to the work of Yi-Zhi Huang, in particular his book Two-Dimensional Conformal Geometry and Vertex Operator Algebras.

Returning to the CFT, the Hilbert space is described by irreducible representations of our affine algebra (left moving and right moving copies) which for a given level k, are paramaterised by highest weight labels. For the example of affine SU(2), the highest weights are characterised by two labels (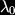, 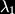) such that 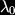+ 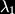= k. The Hilbert space may be written as:Where M is the multiplicity, and the one-loop partition function for this RCFT may be written in terms of the characters, : 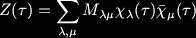It turns out that the characters are modular functions, and are subject to the familiar S and T transformations: 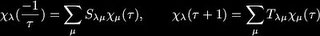Furthermore, the partition function is modular invariant and characterised by its multiplicities, M.

At this point in the talk, Terry had about six minutes remaining and had arrived at what he thought of as the start of his talk, and defined the "modular invariant" he hoped to use to classify RCFTs:

Given some affine algebra at level k, a modular invariant is a matrix M of multiplicities describing the partition function, Z, such that,

Terry told us that these conditions gave rise to RCFTs that are "just barely" classifiable.

Terry finally asked us why bother classifying? Or, in his words, "who cares?" His answer was that the classification leads to interesting results. What more could you want? He gave us the example from Cappelli-Itzykson-Zuber from 1986 of the classification of affine su(2), which is completely classified for the levels, k, 4/k, k/2 is odd, k=10,16,28, and he told us a story he heard twice; once from Zuber about a correspondence he had with Victor Kac, and a second time the same story from Kac - so, he said, it must be a true story. It went like this: After having written down some of the classifications of affine su(2) in 1986, Zuber wrote to Kac about the results, who replied and pointed out the classification for k=10, which he said contained some exceptional numbers - literally numbers he thought came from the exceptional group E_6. Zuber said he didn't understand Kac nor pay it much heed until someone else repeated it years later and he dug out the letter, headed to the library and confirmed that all the numbers appearing in the classification do indeed have an intimate and mysterious (to this day...) relation with the groups A, D, E, and the symmetries of their Dynkin diagrams. At this point Terry bemoaned the fact that God was manifestly not benevolent since he insisted on making 2 a prime number...Terry's discomfort with 2 didn't seem justifiable until later on when he mentioned that his wife is expecting twins (excuse me for this weak pun) so I just put two and two together... :)

So the ADE-classification arises mysteriously from modular invariants, so that's why to classify RCFTs: because they might be interesting.