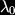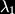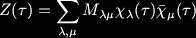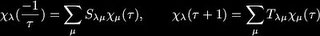Kallosh on Attractors

Yesterday we heard the first of three different talks from Renata Kallosh. Her first chosen specialist subject was innocuously titled BPS and non-BPS Black Hole Attractors. This first talk really was for the back row of the audience at our school, where all the experts were sitting. Perhaps due to the time constraint, quantities were not defined and many ideas were assumed to be known by the audience. Unfortunately there is much work for me to do. At one point she paused and said to the audience:

"So far I was a bit sketchy...but this is something you can read. This is a known result."

Well this is true enough, so here are the references for Kallosh's first talk (just 1 hour):

Black holes and critical points in moduli space by S. Ferrara, G. W. Gibbons and R. Kallosh

Non-Supersymmetric Attractors in String Theory by P.K. Tripathy and S. P. Trivedi

The non-BPS black hole attractor equation by R. Kallosh, N. Sivanandam and M. Soroush

The Symplectic Structure of N=2 Supergravity and its central extension by A. Ceresole, R. D'Auria and S. Ferrera

E(7) Symmetric Area of the Black Hole Horizon by Renata Kallosh, Barak Kol

STU Black Holes and String Triality by Klaus Behrndt, Renata Kallosh, Joachim Rahmfeld, Marina Shmakova, Wing Kai Wong

Calabi-Yau Black Holes by Marina Shmakova

It would have been good to know these papers well before the talk began and as you can imagine the school degenerated to a workshop for the experts during this talk. However there were plenty of interesting things for us beginners to pick up. Such as that N=2 special geometry is useful and that symplectic invariants are useful. I'll try and reproduce my beginner's conception of special geometry in this post, mostly with the help of Christiann Hofman's masters' thesis, Dualities in N=2 String Theory (you can find the link near the bottom of the page).

Special geometry is the name given for the geometry associated to the scalar couplings of the vector and hypermultiplets of theories involving 8 supercharges, although the original use of the name was restricted to N=2, vector multiplets and four dimensions. Recall that the vector multiplet is an irreducible multiplet of super Yang-Mills theory, it is the enhancement of the gauge field to the supersymmetric setting, and has field content: Where X is a complex scalar, omega is a pair of spinors, Y is a triplet of scalars (arranged in an anitsymmetric 2 by 2 matrix) and A is a real gauge boson. For reference the hypermultiplet, when there are no central charges contains the fields: Here, A is a pair of scalar doublets, and zeta is a pair of spinors. When we include gravity in our supersymmetric gauge theory setting we find the metric is enhanced to the gravity multiplet, or Weyl multiplet, consisting of the metric and two fermionic fields of spin 3/2 called gravitini. These gravitational fields can couple to the content of the vector and hyper multiplets. Furthermore an additional vector multiplet is required if we wish to break auxillary gauge symmetries (see Lagrangians of N=2 supergravity-matter systems by de Wit, Lauwers and Van Proeyen). Only the vectors have physical significance, the remainder of the multiplets are auxillary fields. So if we commence with n vector multiplets from our super Yang-Mills theory, and then we include gravity to construct a sensible local theory, we find we require n+1 gauge fields. These gauge fields are the equivalents of our familiar Maxwell gauge field in electromagnetism, and including the dual fields we have 2(n+1) fields which are transformed into each other by the action of the symplectic group Sp(2n+2,R). The flux integrals of the field strengths and their duals give us electric, q, and magnetic, p, charges, and the symplectic transformation is interpreted as the generalization of electric-magnetic duality. So far, so good. But we neglected to mention that we also have n scalar fields which do not transform in such a well-mannered way under the symplectic group action. A suitable projective coordinate reparameterisation (giving us n+1 scalars) will, however, do the job, see Mohaupt's review Strings, higher curvature corrections and black holes for the overview. The scalars of the Lagrangian may be thought of as coordinates and, under the restrictions of supersymmetry, the geometry of the complex symplectic vector space C(2n+2)associated to the scalar coordinates is called special geometry. We end up with coordinates on our manifold, coming from the prepotential and the projective coordinate which do transform as a symplectic vector. However symplectic geometry is a little different from Riemannian geometry, for example symplectic manifolds have no local invariants like curvature.

If, like me, you have never come across any of this technology before you can see that there is plenty of work to do. Especially in picking up terminology and generic constructions. But don't despair! Take heart, all the experts at the school in Frascati presented some very pretty results (I was able to understand this from the joy in their eyes - inc omcing to this conclusion I have assumed the sanity of the speakers...) and it would seem the end result is worth the work.

Attractors

Last Monday and Tuesday saw the start of the Winter school on Supersymmetric Attractor Mechanism here in Frascati. I have already described a little of the content of Per Kraus' talks, but we also have had a series of talks by his frequent collaborator Finn Larsen. Larsen has given three talks under the title Introduction to Attractors with applications to Black Rings and based upon his paper with Kraus: Attractors and Black Rings. At some point there will be a video online. At least one was made, and it seems there is a certain attractor mechanism for all real world content to eventually stabalise on the internet, so it seems fair to expect it will appear one day. I'll let you know if I hear anything.

If on a Winter's Night a Physicist...

So, I find myself in Frascati, just 20km south-east of Rome attending SAM 2006 (School on the Attractor Mechanism). This is my first visit to Italy, and so very exciting for me (food, coffee, wine, olives, historic sites, art, physics...). There are 30 or so of us here at the Instituto Nazionale di Fisica Nucleare, where all the roads are named after famous theoretical physicists! The high energy bulding is on Via P. Dirac, which at some point turns into Via R. Feynman, a nice continuity. There are also roads for Pauli, Heisenberg, Schrodinger, Planck and others, but no Via Einstein! Of course the institute itself lies on the main road named after Enrico Fermi, so he doesn't appear on the campus map either, but that's okay.

The school was billed for beginners, and that is why I am here. Yesterday and today, we heard from Per Kraus and Finn Larsen. Kraus talked under the title "Black Hole Entropy and the AdS/CFT Correspondence" and I hope there will eventually be a video of the talk available online, but we shall see... For the impatient you can alreadywatch/listen to Kraus giving a talk based around his papers Microscopic Black Hole Entropy in Theories with Higher Derivatives and Holographic Gravitational Anomalies both with Fin Larsen. But I think the video of the three hour talk from our school will be much more elementary and welcoming. Hopefully I can make some comments about Fin Larsen's complementary talks in a later post.

Kraus began by telling us about the BTZ black hole (so-called for Banados, Teitelboim and Zanelli), emphasising the point that only for the BTZ black hole does a precise agreement occur between the microscopic and macroscopic counts of black hole entropy . The BTZ black hole is a 3-dimensional black hole similar to the Kerr solution, for a review see Carlip's The (2+1)-Dimensional Black Hole. It lives in three dimensional anti de Sitter space, AdS_3, a space with negative cosmological constant. Identifications in AdS_3 give rise to the BTZ black hole.

AdS_3 can be realised as a hyperboloid in a signature (+,+,-,-), i.e.. This is the Sl(2,R) group manifold. The BTZ black hole can be analysed by looking at the conjugacy classes of Sl(2,R). There are three conjugacy classes: hyperbolic, elliptic and parabolic, with the BTZ black hole sitting in the hyperbolic conjugacy class. Kraus, Samuli Hemming and Esko Keski-Vakkuri have written about this in Strings in the Extended BTZ Spacetime, see section 2. An identification is made with the conjugating elements and the left and right moving temperature, and we move into a thermodynamic setting. Mass, angular momentum, entropy formulae follow, and the equivalence of a thermal AdS_3 background with a BTZ upto various modular transformations in each case.

Kraus considered spacetimes whose near horizon geometry (when r approaches the event horizon, and considering only the dominant terms) factorises into AdS_3 x X x S^p, where X is an unspecified geometry (see Strominger's Black Hole Entropy from Near-Horizon Microstates for the motivation for looking at this geometry). Kraus demonstrated the equivalence of the Wald formula, for finding the entropy from a Lagrangian which includes higher-derivative corrections, with the Cardy density of states formula for a CFT for theories which have a general diffeomorphism invariance. Through this equivalence the exact entropy (i.e. including corrections) is derived solely from knowing the central charges of the theory. Furthermore Kraus presented a variational principle to give the central charge for some Lagrangian with higher derivative terms. In his final talk he looked at the use of gravitational anomalies for learning about the pictures on either side of AdS/CFT.

Kraus used two main examples to illustrate his talk:

D1-D5-P on T^4 x S^1 or K3 x S^1

M5 branes wrapped on 4-cycles in M-theory on CY_3 x S^1

He demonstrated how the BTZ black hole appears in each case and compared the entropy calculations in each case. The D1-D5-P entropy (Strominger and Vafa) is in exact agreement with the macroscopic Bekenstein-Hawking entropy, while the M5 branes' microscopic entropy (Maldacena, Strominger and Witten) gives a central charge consisting of two parts, the highest order part agreeing with the macroscopic count and the remainder being due to the presence of higher derivative terms in M-theory. I refer you to the two papers with Larsen linked to earlier to see the full application of the method with these examples in mind.

Classifying Rational Conformal Field Theories

Yesterday afternoon was quite a chilly day in London, the kind of day when being crammed into a packed and warm lecture room below ground level in the basement of Queen Mary college from where you can hear the tube rattle by was quite an attractive prospect. So at three in the afternoon yesterday that's where I and other London theoretical physicists gathered to hear Terry Gannon talk about "The classification of RCFTs".

First off, it gives me great pleasure to report to you that the "damn book" is finished :) after five years of hard slog Terry's book, Moonshine Beyond the Monster and available to buy from the 31st August, 2006. Hurrah. There's an excellent documentary by Ken Burns on the American Civil War that took longer to make than the war itself, I have no doubt that it will take me inestimably longer to understand this 538 page book than it took to write. Fortunately noone died in the making of the book, to the best of my knowledge. For some history of the Monster see Terry's Monstrous Moonshine: The First Twenty-Five Years.

Terry described his approach to trying to classify Rational Conformal Field Theories (you could look at Wikipedia for a brief definition of a RCFT, or a much better idea might be to start learning about CFT from scratch with Paul Ginsparg's Les Houches lectures, Applied Conformal Field Theories or Krzysztof Gawedzki's Lectures on Conformal Field Theory) by searching for invariants of the chiral algebra, or Frobenius algebra, that underlies the RCFT. By way of comparison, Terry said that the very succesful classification of the Lie algebras rested upon the invariant of the Dynkin diagram. But what invariants are worth considering, whose discovery will tell us most of the information about the algebra? Terry suggested two:

modular invariants (i.e. partition function on the torus)

NIM representations (i.e. partition function on the cylinder)

But he only had enough time to talk a little about the first and describe to us the modular functions that appear.

To commence one must settle upon a chiral algebra, or a vertex operator algebra, and Terry told us that some very nice choices are the affine Kac-Moody algebras (see Fuchs' Lectures on conformal field theory and Kac-Moody algebras section 16 for the definitions). A level, k, must also be picked. We were told that one way to imagine a chiral algebra is as a complexification, or 2-dimensionalisation, of a Lie algebra. If we denote all the objects appearing in a Lie algebra by a tree diagram, having all the properties of the Lie bracket at the branch (i.e. antisymmetric...) then the complexified version of the algebra turns each of the branches of the tree diagram into a cylinder: For more about this way of complexifying to get loop algebras we were referred to the work of Yi-Zhi Huang, in particular his book Two-Dimensional Conformal Geometry and Vertex Operator Algebras.

Returning to the CFT, the Hilbert space is described by irreducible representations of our affine algebra (left moving and right moving copies) which for a given level k, are paramaterised by highest weight labels. For the example of affine SU(2), the highest weights are characterised by two labels (, ) such that + = k. The Hilbert space may be written as:Where M is the multiplicity, and the one-loop partition function for this RCFT may be written in terms of the characters, : It turns out that the characters are modular functions, and are subject to the familiar S and T transformations: Furthermore, the partition function is modular invariant and characterised by its multiplicities, M.

At this point in the talk, Terry had about six minutes remaining and had arrived at what he thought of as the start of his talk, and defined the "modular invariant" he hoped to use to classify RCFTs:

Given some affine algebra at level k, a modular invariant is a matrix M of multiplicities describing the partition function, Z, such that,

Terry told us that these conditions gave rise to RCFTs that are "just barely" classifiable.

Terry finally asked us why bother classifying? Or, in his words, "who cares?" His answer was that the classification leads to interesting results. What more could you want? He gave us the example from Cappelli-Itzykson-Zuber from 1986 of the classification of affine su(2), which is completely classified for the levels, k, 4/k, k/2 is odd, k=10,16,28, and he told us a story he heard twice; once from Zuber about a correspondence he had with Victor Kac, and a second time the same story from Kac - so, he said, it must be a true story. It went like this: After having written down some of the classifications of affine su(2) in 1986, Zuber wrote to Kac about the results, who replied and pointed out the classification for k=10, which he said contained some exceptional numbers - literally numbers he thought came from the exceptional group E_6. Zuber said he didn't understand Kac nor pay it much heed until someone else repeated it years later and he dug out the letter, headed to the library and confirmed that all the numbers appearing in the classification do indeed have an intimate and mysterious (to this day...) relation with the groups A, D, E, and the symmetries of their Dynkin diagrams. At this point Terry bemoaned the fact that God was manifestly not benevolent since he insisted on making 2 a prime number...Terry's discomfort with 2 didn't seem justifiable until later on when he mentioned that his wife is expecting twins (excuse me for this weak pun) so I just put two and two together... :)

So the ADE-classification arises mysteriously from modular invariants, so that's why to classify RCFTs: because they might be interesting.