Heterotic Geometries, all of them

This week George Papadopoulos talked to us about the results from his latest paper, The spinorial geometry of supersymmetric heterotic string backgrounds, with Ulf Gran and Philipp Lohrmann, from my office. I used to keep a pink penguin on the site as a tribute to Philipp, that one could poke and push off some ice while reading the blog. Happy days. Now I have to treat him with much more respect since he and his collaborators have made use of the fundamental procedure of the spinorial geometry programme (which I will describe below) to produce a list of all the possible background geometries for the heterotic string, up to multiplication by a compact group in some cases.

The talk itself began a little ominously on Wednesday when it was realised that our electronic projector was not available, and instead of us all crowding around George's laptop, he managed to give us a blackboard talk which was impressive both for its clarity and in that he hardly ever looked to his laptop for guidance. However one consequence of this was that hardly any complex equations appeared even though there must have been many more intended, and also the speed of the talk was very good for those taking notes. I wonder if this policy of losing the projector is not something we should take up full time at King's...

George began by motivating the study of the Killing spinor equations by looking at the Euclidean instanton bound. In 4-dimensions,
Where we have completed the square. The bound is saturated when,
When we take the minus sign in the above we have the self-duality conditions on the field strength. Now suppose we wanted a spinorial version of this construction. We would start by coupling the spinor to the field strength forming:
Reproducing the equivalent of the Euclidean action above we have another formulation for the instanton bound, but now in terms of spinors,
Normalising the bound is attained if, These are the supergravity Killing spinor equations arrived at by considering the instanton bound.

Having motivated the Killing spinor equations, George moved on to describing the formalism he has developed for helping to solve them. He took us through a 4-dimensional example so we could see the general approach. In 4-dimensions the spin representation is Spin(4) which is the double cover of SO(4), the Euclidean rotation group. There is an isomorphism Spin(4)=SU(2)xSU(2) and there are two different Weyl spinors, with two components in each, which transform under only one of the SU(2)'s. George then described the setting up of a real vector space, whose components will act as a space of forms. In two-dimensions we have two basis elements in the vector space (e_1,e_2). Mimicking the splitting of the Weyl spinors to transform under two different copies of SU(2), we set up a second copy of this vector space by "complexifying" it. The basis of forms is:
We have a basis of two even and two odd forms which corresponds to two different chiralities. If we explicitly write down the gamma matrices using our basis we can get some work done,
I have used a vee for the inner derivative which acts in the opposite way to the exterior derivative; it's destructive while the wedge is constructive, e.g. . These are all we need to solve the Killing spinor equations. We first note that the equation is unchanged under spin(4) transformations, upto a Lorentz transformation on the field strength. That is we may orient the spinor how we wish, in particular we may pick the direction 1 (the "Clifford vacuum" if you like) in the basis: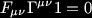
Now we may go back and look hard at our basis for the gamma matrices and write down the combinations that annihilate the vacuum. We use these to define a new (solution) basis: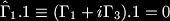
We also have a set of antiholomorphic gamma matrices in this basis which are the complex conjugates of the above. Finally expanding out the Killing spinor equation, by summing over holomorphic and antiholomorphic indices, in this basis leads to some simple expression,
Recalling that the n index gamma matrices are just the antisymmetric combination of the n individual gamma matrices, we see immediately that the first term annihilates the Clifford vacuum. Carrying on thinking about this in terms of a basis of states is fruitful since we also see that the remaining two terms must vanish independently, since they create different "Clifford states". That is the Killing Spinor equations reduce to,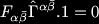
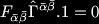So we see from this walkthrough just how simple the equations can become. In particular one can learn about the geometry of a number of setups. In the latest work, linked above, the authors make use of the fact that the heterotic string background resembles a Riemannian manifold, to find all the stability subgroups for the possible numbers and types of Killing spinors. From which the geometry of the background is determined. So impressively it is claimed that all the M-theory geometries corresponding to the heterotic string regime without alpha' corrections have been found. Of course it is not clear what happens to the Killing spinor equation when alpha' corrections are included, but it seems like they will be altered.