A Silver Age in Black Hole Research?

Yesterday afternoon Harvey Reall from Nottingham University came to talk at Imperial College. The talk entitled Black Holes and Extra Dimensions was aimed at masters level students, of which, there was only one in the audience :( However it was a nice talk, and somewhat of a black hole history lesson and worth describing here. Lubos Motl has a report of a very similar talk by Reall which you can find here.

Harvey began by describing the "Golden Age" (so named by Kip Thorne) of black hole research which began in 1963 with the discovery of the Kerr solution, and supposedly lasted until 1973 when the macroscopic black hole entropy formula was discovered by Hawking. The two main achievements of the "age" according to Reall were:

1. The black hole uniqueness theorems
2. Black hole thermodynamics

The uniqueness theorems (for more information you can read David Robinson's "Four decades of black hole uniqueness theorems")in 4 dimensions are twofold; there are separate proofs for the non-rotating and the rotating vacuum solutions. The non-rotating solution is due to Werner Israel (1967) and a more recent proof by Bunting and Masood-ul-Alam (1987) and shows that the only non-rotating, equilibrium solution is the Schwarzschild solution (1917). The only rotating, equilibrium solution is the Kerr solution (1963) as shown by Carter (1971), Hawking (1972) and Robinson (1975). These solutions are described by one (M) and two (M,J) parameters respectively. Generalisations to include the Maxwell field also exist (the Kerr-Newman solution).

Reall spent some time motivating the consideration of extra dimensions. For those interested in string theory he simply said that it is, in his opinion, the best candidate for a theory of quantum gravity. He justified this by saying that the entropy macroscopic entropy formula is the only experimental data that we have for quantum gravity and that microscopic count of entropic degrees of freedom gives matching numbers. For those not so convinced by string theory Reall offered the AdS/CFT (Maldacena 1997) or as he called it the Gauge/Gravity correspondence. The gauge/gravity correspondence was described for the case of a 5D gravity theory in the interior of the cylinder (shown right) being equivalent to a 4D gauge theory on the curved surface of the cylinder - the edge of the cylinder is at infinity by some clever choice of coordinates and three dimensions have been suppressed out of respect for our 4 dimensional universe. In short Reall pointed out that some 4D gauge theories are equivalent to 5D gravitational theories and so we may learn more about QCD calculations by looking at higher dimensional theories.

Reall then moved on to talk about constructing 5D solutions from the known 4D solutions. He began with the black string which was constructed by adding an extra flat dimension to the Ricci flat 4D Schwarzschild solution: 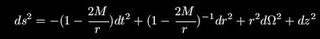This is the black string, it is infinitely long and so has infinite energy. To avoid this we compactify the z direction by identifying z~z+2/piR, the geometry is changed to 4D Minkowski space crossed with a circle. Reall told us that the Black string This is the black string, it is infinitely long and so has infinite energy. To avoid this we compactify the z direction by identifying z~z+2/piR, the geometry is changed to 4D Minkowski space crossed with a circle. Reall told us that the Black string is classically unstable when the radius of compactification, R, is greater than 2M. This is the so-called Gregory-Laflamme instability (1993) and it's endpoint is unknown. However Horowitz and Maeda (2001) conjectured that the endpoint was the non-uniform black string, which has a sine-wave distortion of the event horizon as it moves through its z coordinate. Toby Wiseman showed that these exist using a numerical approach in 2002. The downside is that they lead to decreasing entropy, which is unrealistic!

There is a generalisation of the Kerr solution to D dimensions called the Myers-Perry solution (1986). It has some familiar properties in that it's event horizon has topology S^{D-2} and it is uniquely specified by its mass and its angular momenta (there being [(D-1)/2] angular momenta, where [] means drop the fractions). Another familiar property is that the angular momenta are bounded. Having described this much Harvey Reall asked if there were any other types of higher dimensional black holes, i.e. does the rotating black hole uniqueness theorem still hold in higher dimensions?

Harvey answered that he and Emparan had showed that there existed a different type of black hole in 5 dimensions (2001) - the black ring. This solution is a rotating closed loop of black string, whose gravitational collapse is held at bay by one of its angular momenta. Heuristically the gravitational force is balanced by the centrifugal force. Of course one wonders why a similar rotating black cylinder couldn't exist in 4D...to project to 4D one could set r=0, corresponding to zero mass, hence no 4D equivalent solution to the black ring, at least not in this way. The 5D black ring's second angular momentum is zero and the solution has only 2-parameters with topology S^1 cross S^2.

It transpires that for a certain range of angular momentum there are two ring solutions, one small and one large. So together with the Myers-Perry solution there are some regions of parameters where 3 solutions exist for the given parameters. The uniqueness theorem for rotating black holes is well and truly lost for higher dimensions. The non-rotating uniqueness solution does still hold in higher dimensions (Gibbons, Ida & Shiromizu 2002).

Harvey finished up by telling us about supersymmetric black rings (also known in some circles as: "The Hairy, Tiny Black Hole Donut Theory") which were discovered by Elvang, Emparan, Mateos and Reall (2004); Gauntlett and Gutowski (2004); and Bena and Warner (2004). You can listen to Reall talk about black rings here. The solution is now stabilised by a non-zero second angular momentum (this one rotates the torus about its second circle). The solution has 7 parameters: 2 angular momenta, 3 electric charges, 3 magnetic dipoles and one relation between them all. Also noteworthy is the observation that the dipoles are not conserved, so there are only 5 conserved quantities amongst the seven parameters. The entropy formula is consequently much more complicated than usual but despite this it seems that string theory can still be used to give a correct microscopic count of the solutions degrees of freedom (Cyrier, Guica, Mateos and Strominger 2004), although Reall had some doubts about the count since it seemed to imply that one of the two angular momenta was zero, contrary to the macroscopic solution.

In his final remarks Reall reminded us that the golden age of black hole research was started off by the discovery of the Kerr solution, and he hoped that the silver age would be kicked off by the discovery of the black ring. Personally I'm already worried about naming the third age, since the bronze age is already taken.