Permit me to pass on some brief comments from the beginning of Zagier's talk about the dilogarithm with the caveat that most of this remains beyond my ken. Nevertheless the dilogarithm has been studied by some truly great mathematicians including Euler, Leibnitz, Abel, Lobachevsky, Borel, Ramanujan, and others so if only for historical interest it is nice to look at some of the properties of the dilogarithm in passing.
We are all on first name terms with the logarithm function (that's log to you and me):
 But perhaps not so well known is it's relation the dilogarithm:
But perhaps not so well known is it's relation the dilogarithm: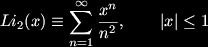 There are plenty of others, which are specific values, s, of the polylogarithm, or Jonquiére's function,
There are plenty of others, which are specific values, s, of the polylogarithm, or Jonquiére's function, 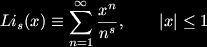 Zagier told us that there are only 8 closed forms for the dilogarithm, some of which include the golden ratio,
Zagier told us that there are only 8 closed forms for the dilogarithm, some of which include the golden ratio, The only irrationals on the left hand side are powers of the golden ratio. We might look for properties of the dilogarithm that are similar to those we know of the logarithm, for example we know that,
The only irrationals on the left hand side are powers of the golden ratio. We might look for properties of the dilogarithm that are similar to those we know of the logarithm, for example we know that,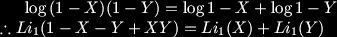 Zagier told us that there was no simple equivalent of this for the dilogarithm, but that we did have a formula, named for Abel even though it had been discovered by others before him (Spence, 1809) and after him (Lobachevsky),
Zagier told us that there was no simple equivalent of this for the dilogarithm, but that we did have a formula, named for Abel even though it had been discovered by others before him (Spence, 1809) and after him (Lobachevsky), Zagier told those of us taking notes in the audience to just write "junk" instead of the right-hand-side of the above, however, he stressed that the order of the left-hand-side terms was important. I think practitioners of this art tend to normalise their dilogarithm functions into the Rogers L-function, which gets rid of the junk. There are a number of useful identities for the dilogarithm two of which are,
Zagier told those of us taking notes in the audience to just write "junk" instead of the right-hand-side of the above, however, he stressed that the order of the left-hand-side terms was important. I think practitioners of this art tend to normalise their dilogarithm functions into the Rogers L-function, which gets rid of the junk. There are a number of useful identities for the dilogarithm two of which are, These lead to equivalent forms of the five-term equation via X ~ 1/X ~ 1-X ~ 1/(1-X) ~ 1-(1/X) ~ X/(X-1). Furthermore if you define a junk-removing functional equation:
These lead to equivalent forms of the five-term equation via X ~ 1/X ~ 1-X ~ 1/(1-X) ~ 1-(1/X) ~ X/(X-1). Furthermore if you define a junk-removing functional equation: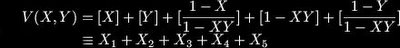 Then this equation has a modulo 5 symmetry,
Then this equation has a modulo 5 symmetry, Try it and see!
Try it and see! Zagier went on to look at the Bloch-Wigner dilogarithm, whose five-term equation is equal to zero and to give an argument in terms of the volume of tetrahedra in a hyperbolic 3-space modulo PSL_2(C) about why it should be zero. It sounded very nice, but I can't say I understood. For those interested the argument is given in section four of sixth set of notes by Matilde Lalin from classes given by Fernando Rodriguez Villegas called "Topics in K-Theory and L-functions". Those interested in seeing many more five-term functional equations should look through Kirillov's Dilogarithm Identities. For an introduction to dilogarithms Maximon's article seems a good place to commence.
Zagier talked fluently, rapidly and energetically about many more topics, such as the Bloch group (if you google Bloch group you may not find much helpful information but you will come across Dr. Bloch's group page), the five-term equation related to the Schrodinger equation for a cubic potential, K-theory (in particular K_3) and also rational conformal field theory, where he spoke with great enthusiasm of the recent conjectures of Werner Nahm. He never once, to my knowledge, resorted to rioting to extend his talk.







6 comments:
This is truly wonderful stuff. My friend sent me, for a birthday present, some jpg's of an article by Zagier from an old (1988) number theory collection. Alas I promptly deleted much of them while trying to organize my inbox. However some research uncovered the source and I've ordered a copy of the book. Thanks for posting your notes and sorry about the riots.
Brad Wood, was it you? Are you responsible for the riots? I hope I've misunderstood for the purposes of gentle comedy :)
Thanks for the nice comments.
Best wishes,
I think it's Zagier that coined the phrase: "The dilogarithm is the only function that has a sense of humour". Has he said that because of the intrinsic characteristics of the function? Or maybe I'm just missing a pun or something....
William Spence, after whom the function was named by early writers in the field, was a Scottish mathematician working in the early nineteenth century.
I hated math and formulas when I was at school but when I was at college I noticed that it is so interesting and now I'm scientist.
Your blog is outrageous! I mean, Ive never been so entertained by anything in my life! Your vids are perfect for this. I mean, how did you manage to find something that matches your style of writing so well? Im really happy I started reading this today. Youve got a follower in me for sure!
Post a Comment